Établir des prévisions de ventes fiables est essentiel pour une entreprise car les ventes prévisionnelles vont notamment déterminer les moyens humains, matériels et financiers que l’entreprise doit mettre en œuvre pour les atteindre.
La réalisation des prévisions de ventes nécessitent de prendre en compte des critères multiples tels que l’état général de l’économie, le type de produit commercialisé, la taille et l’état du marché de produit, la concurrence, et éventuellement la saisonnalité du produit (exemple : les maillots de bain).
Plus d’explications ci-dessous lors de votre BTS en alternance ou d’une autre filière de notre école.
I – Les différents types de prévisions
Deux types de prévisions peuvent être utilisés par les entreprises :
– la prévision individuelle client par client
– la prévision statistique.
A. La prévision individuelle client par client
Cette prévision est très fine puisqu’elle est réalisée client par client. Elle nécessite une connaissance élevée de chacun d’eux.
L’utilisation de ce type de prévision doit être adaptée suivant le bien vendu par l’entreprise :
– le bien vendu est un bien d’équipement
– le bien vendu est un bien consommable
Si le bien vendu est un bien d’équipement, cela signifie que le volume vendu est faible mais que le prix unitaire de vente est élevé (peu de biens mais d’une valeur unitaire élevée). La prévision intègre pour chaque client la probabilité de vendre le bien (appelé parfois taux de réussite).
Exemple : l’entreprise compte vendre 50 machines à laver à un grand hôtel au prix unitaire de 500 euros. Le commercial de l’entreprise estime que la probabilité que cette vente se fasse est de 80%. Par conséquent, le chiffre d’affaires estimé est de 80% x (500 € x 50 machines) soit 20 000 €.
Si le bien vendu est un bien consommable, cela signifie que le volume vendu sera important mais que le prix unitaire de vente est faible (ou en tout cas plus faible que celui d’un bien d’équipement). Deux méthodes de prévisions peuvent être alors utilisées de manière combinée:
– Pour les principaux clients de l’entreprise, la méthode de prévision individuelle telle que nous l’avons déjà présenté pour les biens d’équipement sera utilisée ;
– Pour les autres clients de l’entreprise, la méthode statistique que nous allons présenter ci-après sera utilisée.
B. La prévision statistique
La prévision statistique s’appuie sur deux familles de méthodes :
– Les méthodes explicatives : ces méthodes se concentrent sur l’établissement de liens entre des variables à prévoir et des variables explicatives. A titre d’exemple, nous pouvons citer par exemple comme variable à prévoir les ventes d’un produit et comme variable explicative le budget publicité alloué pour promouvoir ce produit.
– Les méthodes extrapolatives : ces méthodes consistent à projeter dans le futur des données présentes et passées. A titre d’exemple, cela tient à dire que le chiffre d’affaires futur est en partie lié au chiffre d’affaires passé et présent.
Signalons que l’utilisation des méthodes statistiques supposent des populations relativement grandes : prévoir le chiffre d’affaires d’un produit vendu en très faible quantité est plus compliqué que celui vendu en grande quantité.
II – Les prévisions statistiques
A. La corrélation entre deux variables
On parle de corrélation entre deux variables lorsqu’une d’elle dépend de l’autre.
La corrélation peut être positive : la variable A varie dans le même sens que la variable B. Exemple : la vente de maillots de bains varie dans le même sens que le nombre de jours de soleil.
La corrélation peut être négative : la variable A varie en sens inverse de la variable B. Exemple : la vente de maillots de bains varie en sens inverse du nombre de jours de pluie.
La corrélation peut être nulle : la variable A varie indépendamment de la variable B. Exemple : la vente de maillots de bains ne dépend pas du nombre de voitures.
Ces réflexions et exemples pratiques peuvent se retrouver dans la formalisation mathématique de la corrélation :
avec :
r = coefficient de corrélation
X i = ( – )
Y i = ( – )
Pour illustrer nos propos, réalisons un exemple.
Supposons que l’entreprise souhaite étudier l’impact de sa publicité sur ses ventes. Elle recueille les informations suivantes de son département commercial :

Nous pouvons déjà dresser le graphique montrant l’évolution du CA en fonction de la publicité :
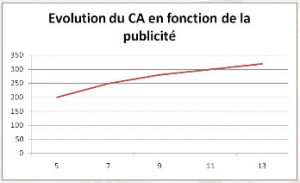
Le graphique permet de mettre en avant le fait que le CA a l’air corrélé de manière positive à la publicité.
Afin de confirmer ce fait, nous allons déterminer le coefficient de corrélation entre les deux variables. Il convient d’établir le tableau suivant au préalable :
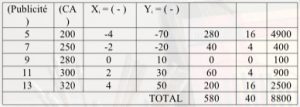
= (5+7+9+11+13) / 5 = 45 / 5 = 9
= (200+250+280+300+320) / 5 = 1350 / 5 = 270
Par conséquent, nous pouvons en déduire le coefficient de corrélation r :
= 580 / = 0,978
Le coefficient de corrélation confirme ce que nous avons déduit de par l’étude du graphique. Ainsi, le coefficient de corrélation est très proche de 1, ce qui signifie que l’évolution du CA est très fortement dépendante de l’évolution de la publicité.
Signalons à cet effet que le coefficient de corrélation peut évoluer entre -1 et 1. Ainsi si le coefficient de corrélation est négatif, cela signifie que les deux variables ne sont pas corrélées. Au contraire, si le coefficient de corrélation est positif, cela signifie que les deux variables sont corrélées. Si le coefficient de corrélation est nul, cela signifie que les deux variables ne sont pas corrélées.
B. L’ajustement entre deux variables
Le coefficient de corrélation permet de voir si une variable dépend d’une autre. Cependant, la seule utilisation du coefficient de corrélation ne permet pas de déterminer le niveau d’une variable par rapport au niveau d’une autre. Si on reprend notre exemple précédent, cela signifie que le coefficient de corrélation ne peut pas à lui seul donner le montant de CA si le budget publicité s’établissait désormais à 15 K€. La seule chose que le coefficient de corrélation pourrait indiquer est que si le budget publicité augmente le CA augmente, mais sans avoir une estimation de ce CA.
L’ajustement permet de pallier à ce manque.
Deux méthodes d’ajustement existent :
– La méthode des moindres carrés
– La méthode de Mayer
Ces méthodes sont différentes mais présentent un point commun très important. L’une comme l’autre permet à celui qui les emploie d’obtenir l’équation d’une droite de type y = ax + b avec y la variable à expliquer et x la variable explicative.
La méthode des moindres carrés
L’équation de la droite des moindres carrés est de type :
y = ax + b
avec
a = et b =
avec
n le nombre d’observations
Supposons que l’on cherche à déterminer le CA prévisionnel à partir d’un historique de CA tels que :
| Année | CA en K€ |
| 2011 | 1000 |
| 2012 | 1200 |
| 2013 | 1350 |
| 2014 | 1420 |
Déterminons l’équation de la droite des moindres carrés à l’aide de cet historique.
Il s’agit de trouver, par l’équation d’une droite d’ajustement d’une série de chiffres d’affaires, la valeur des chiffres d’affaires suivants par le calcul. On sait que toute droite a pour équation y = ax + b où a est le coefficient directeur qui indique la pente de la droite et b est l’ordonnée à l’origine.
La droite des points extrêmes
La méthode des points extrêmes peut être utilisée lorsque la série est régulièrement croissante ou décroissante, et que l’on s’attend à une même tendance dans la variation des données. Cette méthode consiste à prendre la première et la dernière valeur de la série et à résoudre le système d’équations. On sait que toute droite a pour équation y = ax + b.
x i correspond aux années ; y i correspond aux chiffres d’affaires.
Une unité commerciale nous a communiqué les chiffres d’affaires réalisés les années précédentes :
| Xi (années) | Yi (Chiffre d’affaires) |
| N-5 (1) | 512 000 |
| N-4 (2) | 527 000 |
| N-3 (3) | 550 000 |
| N-2 (4) | 586 000 |
| N-1 (5) | 587 000 |
| N (6) | 600 000 |
Il faut tout d’abord renommer les années en partant de 1 pour la plus ancienne.
On ne prend en compte que la première et la dernière année pour le calcul de d’équation de la droite d’ajustement.
On obtient :
Y 1 -> 512 000 = 1a + b
Y 2 -> 600 000 = 6a + b
On peut ensuite résoudre le système d’équations pour trouver a :
600 000 = 6a + b
–
512 000= 1a + b
88 000=5a
88 000/5 = a
17 600 = a
A présent on peut calculer b. Il suffit de remplacer a par la valeur trouver dans l’une des deux équations :
b = 512 000 – a = 512 000 – 17 600 = 494 400
y = 17 600x + 494 400
Pour trouver le chiffre d’affaires prévisionnel pour N+1, il suffit de remplacer x par le numéro de l’année suivante dans l’équation de la droite d’ajustement :
CA de N+1 = 17 600*7+ 494 400 = 617 600
Ce cours de gestion de prévisions des ventes sera enseigné en BTS NDRC, BTS MCO, BTS PI et BTS GPME.
Mis à jour le 12 décembre 2023


